2.2 Rewriting Logic and System Modules

The type of rewriting typical of functional modules terminates with a single value as its outcome. In such modules, each step of rewriting is a step of replacement of equals by equals, until we find the equivalent, fully evaluated value. In general, however, a set of rewrite rules need not be terminating, and need not be Church-Rosser. That is, not only can we have infinite chains of rewriting, but we may also have highly divergent rewriting paths, that could never cross each other by further rewriting.

The essential idea of rewriting logic [37] is that the semantics of rewriting can be drastically changed in a very fruitful way. We no longer interpret a term t as a functional expression, but as a state of a system; we no longer interpret a rewrite rule t --> t' as an equality, but as a local state transition, stating that if a portion of a system's state exhibits the pattern described by t, then that portion of the system can change to the corresponding instance of t'. Furthermore, such a local state change can take place independently from, and therefore concurrently with, any other nonoverlapping local state changes.

Of course, rewriting will happen modulo whatever equational structural axioms the state of the system satisfies. For example, the top level of a distributed system's state does often have the structure of a multiset, so that we can regard the system as composed together by an associative and commutative state constructor.

We can represent a rewrite theory as a four-tuple R= (Omega,E,L,R), where (Omega,E) is a theory in membership equational logic, that specifies states of the system as an abstract data type, L is a set of labels, to label the rules, and R is the set of labeled rewrite rules axiomatizing the local state transitions of the system. Some of the rules in R may be conditional [37].

Rewriting logic is therefore a logic of concurrent state change. The logic's four rules of deduction--namely, reflexivity, transitivity, congruence, and replacement (see Section 4.2.1)--allow us to infer all the complex concurrent state changes that a system may exhibit, given a set of rewrite rules that describe its elementary local changes. It then becomes natural to realize that many reactive systems so specified should never terminate, and that a system may evolve in highly nondeterministic ways through paths that will never cross each other.

The most general Maude modules are system modules. They specify the initial model T_R of a rewrite theory R [37]. This initial model is a transition system whose states are equivalence classes [t] of ground terms modulo the equations E in R, and whose transitions are proofs alpha: [t] --> [t'] in rewriting logic--that is, concurrent computations in the system so described. Such proofs are equated modulo a natural notion of proof equivalence that computationally corresponds to the "true concurrency" of the computations (for a detailed construction of T_R see Section 4.2.2).

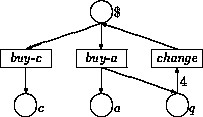
As a first example of a system module, we specify a simple concurrent system, namely a vending machine, as a Petri net. Petri nets have a straightforward rewriting logic semantics as initial models of their associated rewrite theories [37]; therefore, this example illustrates a general method to give executable formal specifications in Maude to Petri nets, a method that can also be naturally extended to high-level algebraic Petri nets [56]. Our Petri net represents a vending machine to buy cakes and apples; a cake costs a dollar and an apple three quarters. Due to an unfortunate design, the machine only accepts dollars, and it returns a quarter when the user buys an apple; to alleviate in part this problem, the machine can change four quarters into a dollar. We can represent graphically such a machine in the conventional way as follows.

The so-called places of this net are cakes, apples, quarters, and dollars, denoted in the picture by circles labeled, respectively, by c, a, q, and $. In each of these places several tokens can be placed. We can therefore think of the places as slots of our machine, in which units of a certain kind appear or disappear. Tokens in one or several of these places can then be consumed by transitions, denoted by rectangular boxes labeled by the transition's name, with incoming and outgoing arcs indicating which tokens are consumed and produced by the transition; we can think of such transitions as the buttons of our vending machine. Such transitions consume tokens from the places in their incoming arcs and produce new tokens in the places of the outgoing arcs. If several tokens must be either consumed or produced in a place, then the corresponding arc indicates the exact number. For example, the change transition requires four quarters to produce a dollar. The vending machine is concurrent because, provided enough tokens are available, we can simultaneously push several buttons and then can simultaneously get the combined results. For example, if we place a dollar and four quarters in the corresponding slots and push the change and buy-c buttons at once, we can simultaneously get a dollar changed and a cake as the result.

The distributed states of the machine, namely the collections of tokens available in the different places, are called markings. They can be naturally regarded as a multiset of places. Using juxtaposition notation, we can for example regard the state with one dollar and four quarters as the multiset $ q q q q. Meseguer and Montanari [44] observed that we can then view the Petri net as an ordinary graph, in which the transitions are the edges, and the nodes are multisets of places. Therefore, as a graph, this net has the following arcs:

buy-c :	$ --> c
buy-a :	$ --> a q
change :	q q q q --> $

The expression of this Petri net in rewriting logic is now obvious. We can view each of the labeled arcs of the Petri net as a rewrite rule in a rewrite theory having a binary associative and commutative operator __ (multiset union), so that rewriting happens modulo such axioms, that is, it is multiset rewriting. We can gather together the "places" $,q,a,c into a sort Place and view the states of the net, that is, the markings, as elements of a supersort Marking containing Place and endowed with a multiset union operator with empty syntax. The corresponding Maude module then becomes

  mod PETRI-NET is
    sorts Place Marking .
    subsort Place < Marking .
    op __ : Marking Marking -> Marking [assoc comm] .
    ops $ q a c : -> Place .

    rl [buy-c] : $ => c .
    rl [buy-a] : $ => a  q .
    rl [change] : q  q  q  q => $ .
  endm

The rewrite theory (Omega,E,L,R) corresponding to a system module has a signature Omega given by the sorts, subsort relations, and operator declarations, a set E of equations, that is assumed to be decomposed as a union E = A U E', with A a set of axioms to rewrite modulo among those supported by Maude, and E' a set of Church-Rosser and terminating equations modulo A. In the above example A consists of the associativity and commutativity axioms, E' is empty, the label set L contains the labels of the three transitions, and the set of rules R contains the above three rules, each introduced by the keyword rl. One can also define conditional rules¹⁰, introduced by the crl keyword.

A key result about the representation of Petri nets as rewrite theories is that, given two markings M and M' on a net, the second is reachable from the first by a concurrent net computation if and only if the sequent M --> M' is provable in rewriting logic using the rewrite theory associated to the net [37]. Of course, net computations need not be confluent--therefore, they can be highly nondeterministic--and need not be terminating (they just happen to be terminating in this example). Therefore, the issue of executing rewriting logic specifications, such as those for Petri nets, or for system modules in general, is considerably more subtle than executing expressions in a functional module, for which the termination and Church-Rosser properties guarantee a unique final result regardless of the order in which equations are applied as simplification rules.

As we explain in Section 2.6, using reflection the rewriting inference process can be controlled with great flexibility in Maude by means of strategies that can be defined by rewrite rules at the metalevel. However, the Maude interpreter provides a default strategy for executing expressions in system modules. The default strategy applies the rules in a top-down fair way, and is provided by the rewrite command, with keyword rewrite or, in abbreviated form, rew. Since we assume that the equations E in a system module are decomposed as a union E = A U E' with A a set of equational axioms declared as attributes of some operators to rewrite modulo, and E' a set of Church-Rosser and terminating equations modulo A, before the application of each rewrite rule the expression is simplified to its canonical form using the equations¹¹; that is, it is simplified by applying the equations E' modulo A. Then, a rule is applied to such a simplified expression modulo the axioms A according to the default strategy. Since in our Petri net example E' is empty, this equational simplification process before each rule application becomes in this case the identity.

An expression given to Maude with the rew command will be rewritten with the default strategy until no more rules can be applied. Since such a computation in general may not terminate, Maude allows the user to specify the maximum number, enclosed in brackets, of rule applications allowed when executing the rew command. We give below several sample executions for our Petri net module with and without a bound for the rew command.

  Maude> rew $ $ $ $ $ q q q q q .
  result Marking: a a a c c c c

  Maude> rew [1] $ $ $ $ $ q q q q q .
  result Marking: $ $ $ $ $ $ q

  Maude> rew [2] $ $ $ $ $ q q q q q .
  result Marking: $ $ $ $ $ q q a

  Maude> rew [3] $ $ $ $ $ q q q q q .
  result Marking: $ $ $ $ q q a c

  Maude> rew [4] $ $ $ $ $ q q q q q .
  result Marking: $ $ $ q q a c c

Another simple, yet interesting, system module is the following ND-INT module, that provides nondeterministic machine integers and nondeterministic choice.

  mod ND-INT is
    protecting MACHINE-INT .
    sort NdInt .
    subsort MachineInt < NdInt .
    op _?_ : NdInt NdInt -> NdInt [assoc comm] .
    var N : MachineInt .
    var ND : NdInt .
    eq N ? N = N .
    rl [choice]: N ? ND => N .
  endm

In this example we regard a finite set of integers as a nondeterministic integer of sort NdInt, that is, as an integer that could be any of those in the set. Of course, as indicated by the subsort declaration MachineInt < NdInt, singleton sets are just machine integers, that is, they can be viewed as those nondeterministic integers from which any nondeterminism has already been eliminated. Union of nondeterministic integers, denoted _?_ is associative and commutative and obeys also an idempotency equation. Nondeterministic choice is then provided by the choice rule.

Note that, since in membership equational logic the operators in the module are lifted to the kinds, that is, to the error supersorts, we can give expressions the benefit of the doubt and therefore we can perform arithmetic operations on such nondeterministic integers as exemplified by the following Maude executions

  Maude> rew (1 ? 5 ? 2 ? 1 ? 5) + (3 ? 11 ? 7 ? 3 ? 11) .
  result NzMachineInt: 4

  Maude> rew (1 ? 5 ? 2 ? 1 ? 5) * (3 ? 11 ? 7 ? 3 ? 11) .
  result NzMachineInt: 3

  Maude> rew [1] (1 ? 5 ? 2 ? 1 ? 5) * (3 ? 11 ? 7 ? 3 ? 11) .
  result Error(NdInt): 1 * (3 ? 7 ? 11)

  Maude> rew [2] (1 ? 5 ? 2 ? 1 ? 5) * (3 ? 11 ? 7 ? 3 ? 11) .
  result NzMachineInt: 3

  2 = 2 ? 5 = 5

As yet another example of a system module we introduce below the module SORTING for sorting vectors of integers. In this module, such vectors are represented as sets of pairs of integers, with the first component of each pair corresponding to the vector position and the second to the number in that position.

  mod SORTING is
    protecting MACHINE-INT .

    sorts Pair PairSet .
    subsort Pair < PairSet .

    op <_;_> : MachineInt MachineInt -> Pair .
    op empty : -> PairSet .
    op __ : PairSet PairSet -> PairSet [assoc comm id: empty] .

    vars I J X Y : MachineInt .

    crl [sort] : < J ; X > < I ; Y > => < J ; Y > < I ; X >
          if (J < I) and (X > Y) .
  endm

The top level of the state is in fact a set, namely, an element of sort PairSet built up by the associative and commutative operator __. That is, the states are sets P of pairs of integers. For the sake of the example, let us suppose that for any pair < i ; x > in an input set P, i < card(P), and we cannot have two different pairs < i ; x > and < j ; y > in P such that i = j. That is, any input set P is indeed a vector of integers; of course, these requirements on P could have been explicitly specified by declaring a subsort and giving membership axioms imposing the above conditions, but this is inessential for our present purposes.

There is just one conditional rule, labeled sort, that modifies a vector of integers in order to put it into sorted order. The system thus described is highly concurrent, because the sort rule can be applied concurrently to many couples of pairs in the set representing the vector. Any complex concurrent rewriting of the set of pairs will then correspond to a proof in rewriting logic.

Using the rew command, we can use Maude's default interpreter for executing expressions in system modules. The Maude engine then applies the rules in a fair top-down fashion to sort a vector of integers, e.g.,

  Maude> rew < 1 ; 3 > < 2 ; 2 > < 3 ; 1 > .
  result PairSet: < 1 ; 1 > < 2 ; 2 > < 3 ; 3 >

Using the default interpreter we have virtually no control over the application of the rules in the module. In particular, in this example we have virtually no control over the way in which the rule sort is applied. Although not a problem in this case, because this specification happens to be confluent and terminating, in general we may want to control the way in which the rules are applied. Of course, if the specification is nonconfluent or nonterminating it is not only that we might want to have this control but that we need it. As already mentioned, this can be done with strategies. Section 2.6 explains how, using strategies, the rewriting inference process can be controlled in Maude for this example and for a highly nondeterministic example specifying the rules of a game. For this example such strategies correspond to specifying different sorting algorithms guiding where the sort rule should be applied at each point in the computation.

Among the many concurrent systems that we can specify as system modules in Maude, concurrent object-oriented systems are an important subclass. Maude has special syntactic conventions for specifications in this subclass, called object-oriented modules [38]. However, object-oriented modules are entirely reducible to ordinary system modules by a desugaring process that strips away the, very convenient, syntactic sugar. Object-oriented modules are not supported in Core Maude; they are instead supported in Full Maude, the extension of Maude written in Maude itself in which we also support parameterized modules and module expressions. They are discussed in detail in Section 3.2.